Should we build the Causal Experts Network?
Fundamentals
Fundamentals is a set of short articles presenting the basic causal concepts, power tips and secrets to help you jump-start your causal journey. We focus on causal inference and causal discovery in Python, but many resources are universal.The list of topics will grow with bi-weekly frequency.
Available topics:
Two Ideas to Make Your Casual Discovery More Robust
Start learning now!
Free content on causal machine learning & updates on my causal book:
Want to learn fundamental concepts on causality?
Becoming a better (casual) Data scientist in 2023
Start learning now!
Free content on causal machine learning & updates on my causal book:
Want to learn fundamental concepts on causality?
Three amazing resources on TMLE
Start learning now!
Free content on causal machine learning & updates on my causal book:
Want to learn fundamental concepts on causality?
Three amazing resources on double machine learning (DML)
Start learning now!
Free content on causal machine learning & updates on my causal book:
Want to learn fundamental concepts on causality?
Four amazing Causality Resources
Meet Causal Bandits:
Get the latest news on Causal AI in your inbox:
Welcome to Causal python!
Check the latest blog post here:
Free content on causal machine learning & updates on my causal book:
D-Separation
Pearlian causal inference framework is rooted in Bayesian networks. In Bayesian networks (that are probabilistic graphical models) we represent variables as nodes and conditional probabilities between variables as directed edges.
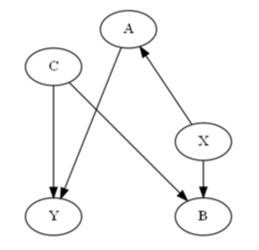
In causal inference nodes also represent variables, but edges represent causal relationships between the variables rather than just conditional probabilities.D-separation is a set of rules that allows us to block a path between two (sets of) variables.There are three basic graphical structures**:
• forks
• chains
• collidersKnowing the three structures, d-separation boils down to the following rules:For any three disjoint sets of nodes X, Y and Z, a path between X and Y is blocked by Z if:• There’s a fork i←j→k or a chain i→ j→ k in this path such that the middle node j∈Z or• There’s a collider i→j ←k on this path such that neither j nor any of its descendants belongs to Z.These rules can be now used to de-confound causal relationships in your data or uncover causal structure (e.g. PC algorithm)._____________** To learn more about these structures check this video or this video.Play with causal structures in the notebook
Causal Discovery
Check the latest blog post here
Defining Causality
People have been thinking about causality over the millennia and across the cultures.Aristotle – one of the most prolific philosophers of ancient Greece – claimed that understanding causal structure of a process is a necessary ingredient of knowledge about this process. Moreover, he argued that being able to answer “why” questions is the essence of scientific explanation. He distinguished four types of causes (material, formal, efficient and final), an idea that might capture certain interesting aspects of reality as much as it might be counter-intuitive to a contemporary scientist or researcher.David Hume, a famous 18th century Scottish philosopher, proposed a more unified framework for cause-effect relationships. Hume starts with an observation that we never experience cause-effect relationships in the world, which leads him to formulating an association-based definition of causality (human mind produces a sense of cause-effect relationships when it gets used to repeatable sequences of events).[Note that this is a very simplified view on Hume's ideas. To learn more check this article]We know that pure associations are not enough to accurately describe causal effects (vide confounding).In order to address this issue and reduce the complexity of the problem, Judea Pearl proposed a very simple and actionable definition of causality:A causes B when B "listens to" AThis essentially means that if we change something in A, we expect to see a change in B.This definition allows us to abstract out ontological complexities and focus on addressing real-world problems.
Assumptions: Positivity
What is positivity assumption?Positivity (also known as overlap) is one of the most fundamental assumptions in causal inference.Simply put, it requires that the probability of treatment, given control variables is greater than zero.Formally:P(T=t | Z=z) > 0(Greater than 0 == positive; hence the name)What is the meaning of this formula?For every value of the control variables, the probability of every possible value of treatment should be greater then 0.Why is this important? Let's see!Let's assume that in our dataset we have 60 subjects described by a single continuous feature Z.Each subject either receives a binary treatment T or not, and each subject has some continuous outcome Y.Importantly, we need to control for Z in order to compute the unbiased effect of the treatment T on the outcome Y.Imagine that, by accident, the treatment was administered only to people whose value of Z is 5 or more. On the other hand, people whose value of Z is less than 5, did not get the treatment.To compute the average treatment effect (ATE) of treatment T, we need to compare the values of the outcomes under the treatment to the values under no treatment:ATE = E[Y(1) - Y(0)]Take a look at the figure below:
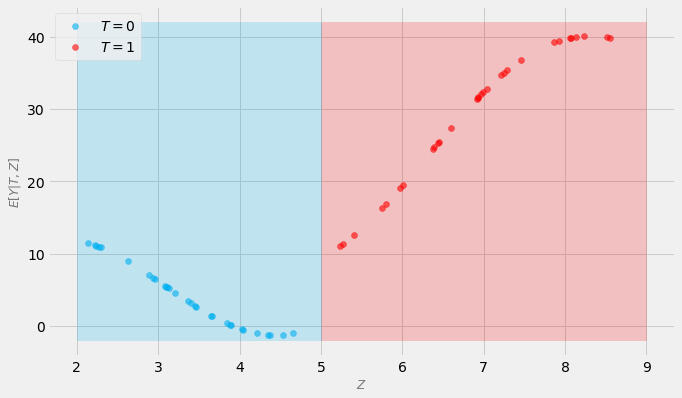
Subjects that got the treatment are marked in red. Subjects that did not get the treatment are marked in blue.Is the probability of each value of treatment greater than zero for each value of Z?Clearly not!So, what’s the problem here?In order to compare the outcomes of treated subjects with the outcomes of untreated subjects, we need to estimate the values for red dots in the blue area (where we have no treatment) and the values of the blue dots in the red area.Whatever model we use for this purpose, it will need to extrapolate.Take a look at the figure below that shows possible extrapolation trajectories (red and blue lines respectively):
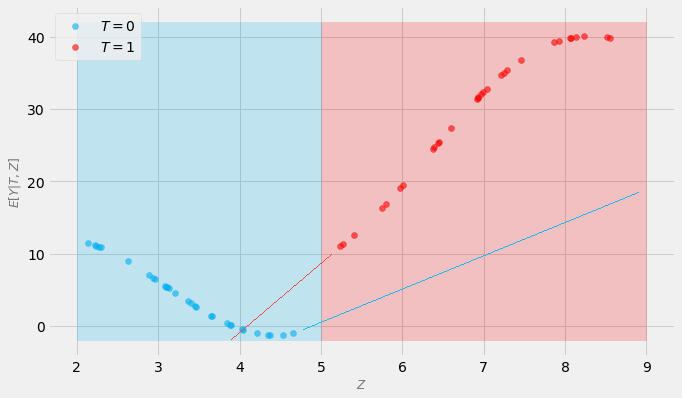
How accurate is it in your opinion?Will it lead to good estimates of the treatment effect?It really hard to answer this question! We can only guess!Compare this to the figure below where positivity assumption is not violated:
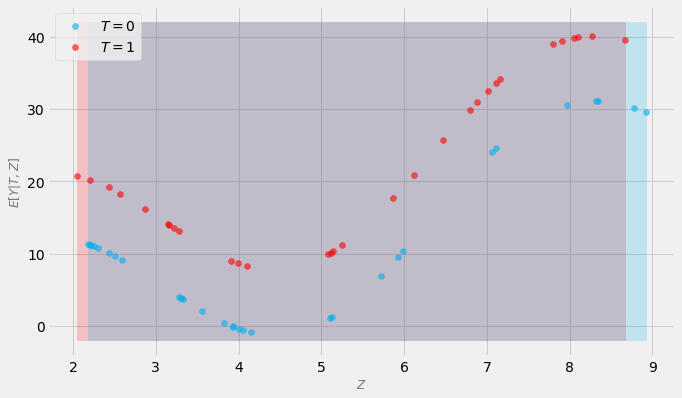
Now, a model has a much easier job to do. It only needs to interpolate.We can reasonably estimate the effect from, without guessing! That’s the essence of the positivity assumption!Naturally, positivity also works in higher dimensional cases (with a caveat that interpolation in high dimension is a problematic concept in itself; Balestriero et al., 2021).
Photo: Ahmet Polat
Structural Causal Models
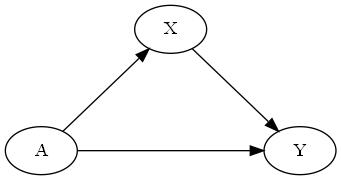
This model can be described by the following set of assignments (traditionally called structural equations):A := fa(εa)
X := fx(A, εx)
Y := fy(A, X, εy)where fs are some arbitrary functions (fx is a function specific to X and so on) and εs are noise terms (imagine a normal distribution for instance). Note that we've omitted εs in the graph for simplicity, but they are an important part of the model.In the SCM nomenclature A, X and Y are called endogenous variables while εs are called exogenous variables (note that they don't have any parent assignments).Some researchers tend to include the graphical representation in the definition of SCM and some don't. The definitions are not entirely consistent in the literature.
Confounding
Confounding is a basic causal concept.Confounding variables influence two or more other variables and produce a problematic spurious association between them. Such an association is visible from purely statistical point of view (e.g. in correlation analysis), but does not make sense from the causal point of view.To learn more check this Jupyter Notebook and this blog post.
Books on Causality
ntroductionRecent years brought a sharp increase in interest in causal methods in the research community and in the industry. One of the challenges that people entering the field face is a lack of standardized resources and terminology. Causality research has been scattered and divided into sub-fields for decades. One of the consequences of this fact is that many newcomers feel overwhelmed and confused when they enter the field.I was in the same spot a couple years ago.In this post I want to share with you six causal books that allowed me to structure and speed-up my causal journey. I hope they will help you achieve the same!And yes, you got it right, you can get 3 of these books for free, 100% legally if you choose so! 😯For every book I’ll provide you with 5 bullet points highlighting the most important topics covered in the book. I’ll also provide you with links to get a copy and/or a free copy of a book if it’s available.If you’re a Python person interested in causality, sign up for my email list here: https://causalpython.io to get free exclusive content and updates on my upcoming causal inference & discovery book right in your inbox!Let’s start!
1. Starting Strong: “The Book of Why”
Figure 1. “The Book of Why” by Judea Pearl and Dana Mackenzie. Image by yours truly.
Figure 1. “The Book of Why” by Judea Pearl and Dana Mackenzie. Image by yours truly.“The Book of Why” by the godfather of modern causality Judea Pearl and his co-author, former mathematician Dana Mackenzie is a starting point for many and not by accident.You can think of it as a comprehensive introduction to the field. It’s a mixture of theory, history, storytelling, math and practical exercises. If that sounds like a lot, don’t worry, it’s really well-structured and fun to read! The authors cover the history of causality, the basic theory behind Pearl’s do-calculus and share inspiring examples of the applications of causal inference in the real life and science. We also get many useful comparisons between do-calculus and potential outcomes frameworks. They will not only let you learn the basics of the latter, but also to grasp the elementary vocabulary that will help you orientate yourself in the broader causal world. Last, but not least the narrative is build around the concept of The Ladder of Causation — a powerful framework that helps the reader to clearly distinguish between associative, interventional and counterfactual modes of analysis.Another great thing about this book is that it’s available as an audiobook!What you’ll learn:History of causality
The Ladder of Causation
Basics of do-calculus
Selected concepts of the potential outcomes framework
Useful applications of causal inferenceGet a copy:Paper (Amazon)
Kindle (Amazon)
Audiobook (Audible)Amazon links in this article are affiliate links. For every purchase made using these links I’ll receive a small amount of the transaction fee that will support my writing. At the same time it does not change the price for you. Thank you!2. Your Turn: “Causal Inference in Statistics — A Primer”
Figure 2. “Causal Inference in Statistics: A Primer” by Pearl, Glymour and Jewell. Image by yours truly.
Figure 2. “Causal Inference in Statistics: A Primer” by Pearl, Glymour and Jewell. Image by yours truly.When I finished reading “The Book of Why” I wanted more! At the same time, I was not sure which direction to take. I asked my network on Twitter for their recommendations. The first reply I got was from Judea Pearl (sic!) who recommended “Causal Inference in Statistics: A Primer” to me. Whose recommendation could be better?It’s a great book with an amazing approach to teaching. It’s relatively short — just a little over 120 pages, yet very content-rich, including exercises.The book is divided into 4 parts:A review of basic statistics and probability,
Introduction to graphical models,
A discussion on interventions,
A discussion on couterfactuals.The book will give you really solid foundations, especially if you follow with the exercises! I want to add that the theory and practice are mostly limited to discrete and linear cases, yet I see this as an advantage. It allows you to focus on what’s important from the causal point of view rather than being distracted by complex math or fancy estimation methods.The book also covers more advanced topics like mediation, direct and indirect effects, probability of sufficiency and necessity and teaches you how to compute counterfactuals by hand (how cool is that?).I read it on my Kindle but a paper version is also available.What you’ll learn:Graphical models
Interventions as graph surgery
Back-door and front-door criteria and inverse probability weighting
Counterfactuals
Mediation, probability of necessity and probability of sufficiencyGet a copy:Paper (Amazon)
Kindle (Amazon)3. Get more perspective: “Elements of Causal Inference”
Figure 3. “Elements of Causal Inference” by Peters, Janzig and Schölkopf. Image by yours truly.
Figure 3. “Elements of Causal Inference” by Peters, Janzig and Schölkopf. Image by yours truly.After finishing “Causal Inference in Statistics: A Primer”, I was hungry for more! In particular, I wanted to learn more about causal discovery.“Elements of Causal Inference” by Peters and colleagues is the first book on our list that goes beyond traditional causal inference and extends to causal structure learning (aka causal discovery). This might sound strange, because the term causal inference is written is glaring large yellow letters on the cover. The reason for this is that the authors use the term in a broader meaning that also includes causal discovery (do you remember what did we say about standardized terminology in the intro? — that’s just a tip of the iceberg!)The book covers differences between purely statistical and causal models, assumptions for causal inference, bi-variate and multivariate models, semi-supervised learning, reinforcement learning, domain adaptation and time series models, all seen through causal lens.Math goes beyond discrete and linear cases and you can meet integrals and derivatives here and there. The authors share some examples and insights from the world of physics — a nice addition to popular examples from the fields of social sciences and epidemiology.Is the book a complete handbook for causal inference and discovery? As the authors state in the introduction — no, rather their “personal taste influenced the choice of topics” (Peters et al., 2017, p. xii) and in my opinion it makes this book really unique!Before we conclude, let me share two more thoughts with you. If you look for a book that is full of real-world use cases and solutions to practical problems —you won’t find it here. If on the other hand you aim at deepening your understanding of the mechanics of causal inference and discovery, in particular in relation to machine learning, this might be a really good shot! 🤘🏼If you’re not sure, don’t worry! You can get this book for free 😯 in a PDF format and check if it’s a good fit for you (link below).What you’ll learn:Theory behind (some of the) causal discovery methods
Causal inference & discovery for bi-variate models
Causal inference & discovery for multivariate models
Causality vs episodic reinforcement learning
Causality and time seriesGet a copy:Paper (Amazon)
Kindle (Amazon)
Free PDF (OAPEN)Causal Python: 3 Simple Techniques to Jump-Start Your Causal Inference Journey Today
Learn 3 techniques for causal effect identification and implement them in Python without losing months, weeks or days…towardsdatascience.com
4. Deep Dive: “Causality — Models, Reasoning and Inference”
Figure 4. “Causality: Models, Reasoning and Inference” (2nd Ed.) by Judea Pearl. Image by yours truly.
Figure 4. “Causality: Models, Reasoning and Inference” (2nd Ed.) by Judea Pearl. Image by yours truly.Pearl’s “Causality: Models, Reasoning and Inference” brings over 400 pages of causal deep dive. The book covers graphical models, d-separation, Bayesian causal models, structural causal models, structural equation models (SEM), model identification, assumptions behind causal inference, complete rules of do-calculus, in-depth discussions on interventions and counterfactuals, probability of causation and more.In addition, the book discusses a bit of causal discovery. Chapter 2 covers two structure learning algorithms proposed by Pearl and Verma: IC and IC*. In many places in the book, you can find comparisons between graph-based approach to causality and Rubin’s potential outcomes framework, which allows you to deepen your understanding of (inter)relations between the two.The last part contains over 60 pages of reflections and discussions with readers.All of this adds up to a very comprehensive resource on causality that you can use as your go-to reference on the topic ⚡⚡⚡What you’ll learn:Assumptions behind causal inference
Do-calculus (in-depth)
Casual discovery (limited scope)
Probability of causation
Interventions and couterfactuals (in-depth)Get a copy:Paper (Amazon)
Kindle (Amazon)5. The World of Econometrics: “Causal Inference — The Mixtape”
Figure 5. “Causal Inference: The Mixtape” by Scott Cunningham. Image by yours truly.
Figure 5. “Causal Inference: The Mixtape” by Scott Cunningham. Image by yours truly.Do you feel like something more practical?Scott Cunningham’s “Causal Inference — The Mixtape” is the first book on the list with the main focus on real-world applications of causal inference methods. The book provides us with a ton of great practical examples of causal inference applications from the fields of economics, social policy, epidemiology and more.The narrative is enriched with frequent references to hip-hop culture and quotes from hip-hop artists (my favorite example is a quote from Chance the Rapper used to explain how to find good instruments when using Instrumental Variables technique ♥️). Each section of the book is accompanied by Stata and R code snippets. Python code is available in the book’s repository and in the online version of the book (link below).The main focus of the book is on the methods popular in contemporary econometrics: regression discontinuity, instrumental variables, difference-in-differences and synthetic control estimator. The book contains just enough math to give you a solid understanding of the discussed methods. Not too much, not too little.The book covers both — randomized and natural — experiments and provides us with a comprehensive overview of potential outcomes framework.🤫Psst! Scott Cunningham is also an author of a popular podcast on causality. You can find it here.What you’ll learn:Natural experiments
Potential outcomes
Regression discontinuity
Instrumental variables
Difference-in-differences & synthetic control estimatorGet a copy:Paper (Amazon)
Kindle (Amazon)
Free Online Book6. A Unifying Framework? “What If?”
Figure 6. “Causal Inference: What If?” by Hernán and Robins. Image by yours truly.
Figure 6. “Causal Inference: What If?” by Hernán and Robins. Image by yours truly.Last, but not least, the sixth book I want to recommend to you comes from Harvard’s Miguel Hernán and James Robins. Both authors are seasoned researchers and well-known figures in the world of epidemiology.The book is divided in three parts:Causal inference without models
Causal inference with models
Causal inference from complex longitudinal dataOut of the six, this is probably the most balanced book in terms of how much space is dedicated to graph-based vs potential outcomes frameworks.The authors provide us with great insights on interactions in the context of interventions, selection bias and more.A part of the uniqueness of the book lies in the discussions of structural nested models, causal survival analysis and causal effects of time-varying treatments. It’s a great read if you want to broaden your horizons!The book comes with code in SAS, Stata, R, Python ♥️ and Julia. Links to all repositories are available on book’s website.Currently the print version is not available. According to the information on Amazon Canada it will be available in June 2023.What you’ll learn:Interactions
Selection bias
Structural nested models
Causal survival analysis
Causal effects of time-varying treatmentsGet a copy:Free PDFWrapping It Up!In this post we discussed six causal books that will get you from beginner to advanced in causality. Each book offers something unique that you cannot find in others. Three of the books mentioned in this article get be read for free — either online or as a PDF.If you want to jump-start your causal journey in Python today, check this post.Good luck with your causal journey 💪 and let me know your thoughts in the comments and/or reach out on LinkedIn!Synthetic controls:October 2022 brought a lot of novelty to Twitter’s Headquarters in San Francisco (and a sink). Elon Musk, the CEO of Tesla and SpaceX became the new owner and the CEO of the company on October 27.Some audiences welcomed the change warmly while others remained skeptical.A day later, on October 28, Musk tweeted “the bird is freed”.How powerful a tweet can be?Let’s see!
Image by Laura Tancredi at Pexels.
ObjectiveIn this blog post we’ll use CausalPy — a brand new Python causal package from
PyMC Developers
(https://www.pymc-labs.io) to estimate Musk’s tweet’s impact on our googling behaviors leveraging a powerful causal technique called synthetic control. We’ll discuss the basics of the method’s mechanics, implement it step-by-step, and analyze potential problems with our approach, linking to additional resources on the way.Ready?
IntroductionEarly November 2022, I had a conference talk scheduled to talk about quantifying effects of interventions in time series data. I thought that it would be interesting to use a real-world example in the presentation and I recalled Musk’s tweet. There was a lot of buzz on the internet around Twitter’s acquisition and I wondered to what extent a tweet related to an event like this can influence our behaviors beyond traditional social media activities, for instance how does it impact how often we Google for “Twitter”?
Embed 1. Elon Musk’s tweet.But first things first.
Causality & ExperimentsCausal analysis seeks to identify and/or quantify the effects of interventions (also known as treatments) on the outcomes of interest. We change something in the world and we want to understand how another thing changes as a result of our action. For example, a pharmaceutical company might be interested in determining the effect of a new drug on a particular group of patients. This might be challenging for a number of reasons, yet the most basic one is that it’s impossible to observe the same patient both taking the drug and not taking it at the same time (this is known as the fundamental problem of causal inference).People figured out many smart ways to overcome this challenge. The one considered a golden standard today is called a randomized experiment (or randomized controlled trial; RCT)¹. In an RCT participants (or other entities in general sometimes called units) are randomly assigned to either the treatment group (with treatment) or the control group (without treatment)².
Causal Python — 3 Simple Techniques to Jump-Start Your Causal Inference Journey Today
Learn 3 techniques for causal effect identification and implement them in Python without losing months, weeks or days…towardsdatascience.comWe expect that in a well-designed RCT randomization will balance the treatment and control groups in terms of confounders and other important characteristics and this approach is usually pretty successful!Unfortunately, experiments are not always available for economic, ethical or organizational reasons among others.What if we…
Image by Engin Akyurt @ pexels.com
Synthetic ControlWhat if we can only observe the outcome under treatment but the control group is not available? Alberto Abadie and Javier Gardeazabal found themselves in this exact situation when trying to asses the economic cost of conflict in Basque Country (Abadie & Gardeazabal, 2003). Their paper gave birth to the method that we discuss today — synthetic control.The basic idea behind the method is simple — if we don’
Books on Causality
Causality as a field is highly heterogenous.When I was starting in the field, I was very surprised to learn that sub-fields of causal inference and causal discovery were almost entirely separated and studied by virtually non-overlapping groups of researchers.Additionally, two main schools of thought in causal inference - one coming from Donald Rubin the other from Judea Pearl - tend to use different vocabulary, making the life of causal student even more difficult.
My curated list of [six causal books]((https://medium.com/@aleksander-molak/yes-six-causality-books-that-will-get-you-from-zero-to-advanced-2023-f4d08718a2dd) is here to help you grasp these differences and find the common denominator among the noise.
This list is not meant to be complete (whatever it means). It's rather a guided tour to help you feel at home in the Causal Wonderland.The six books are:
- The Book of Why
- Causal Inference in Statistics — A Primer
- Elements of Causal Inference
- Causality — Models, Reasoning and Inference
- Causal Inference — The Mixtape
- Causal Inference - What If?Learn more about these books in this blog post.
Congrats!
Next step: Please check your inbox to confirm your email.